최소 공통 조상(Lowest Common Ancestor, LCA)
February 16, 2022
LCA알고리즘이란?
LCA 알고리즘은 Lowest Common Ancestor의 약자로 영어 해석 그대로 어떠한 트리에서 최소 공통 조상을 찾는 알고리즘이다.
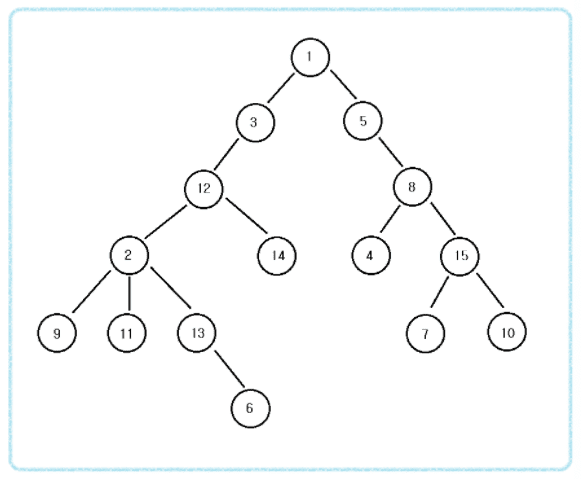
위의 사진에서 두 정점 u,v 의 가장 가까운 조상을 LCA(u,v)라고 한다.
- 예를들어 12와 5의 공통 조상 LCA(12,5)는 1이고, 6과 9의 공통 조상 LCA(6,9)는 2이다.
- LCA 알고리즘은 주로 트리에서 노드와 노드 간의 거리를 구하거나 공통 조상이 누구인지 묻는 문제에서 많이 등장한다.
구현 방법
- 모든 노드에 대한 깊이(depth)를 계산한다.
-
최소 공통 조상을 찾을 두 노드를 확인한다.
- 먼저 두 노드의 깊이(depth)가 동일하도록 거슬러 올라간다.
- 부모가 같아질 때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라간다.
- 모든 LCA(a,b)연산에 대하여 2번의 과정을 반복한다.
코드
public class LCA{
// N은 노드의 개수, K는 조상에 대해 저장하는 값
static int N, K;
// 각 노드의 깊이값을 저장하는 배열
static int[] depth;
// parent[K][V] 는 정점 V의 2^K번째 조상의 정점 번호
// parent[K][V] = parent[K-1][parent[K-1][V]] 이다.
static int[][] parent;
// 인접리스트 정보를 저장하는 tree이다.
static ArrayList<Integer>[] tree;
// 예를 들어 N이 60이라면 2^6 = 64이므로 K값은 6이 됌
static void getK(){
for(int i=1; i<=N; i*=2){
K++;
}
}
// id는 노드번호, cnt는 깊이
static void getDepth(int id, int cnt){
// 1.depth를 기록
depth[id] = cnt;
// 2. 자식들의 depth를 기록
int len = tree[i].size();
for(int i=0; i<len; i++){
int next = tree[id].get(i);
// 아직 깊이를 모르는 상태라면 즉 미방문 노드라면
if(depth[next] == 0){
getDepth(next, cnt+1);
// 2^0 번째 부모 즉 바로위의 부모(첫번째 부모)를 저장하는 것
parent[0][next] = id;
}
}
return;
}
// 부모 채우기 즉 Sparse Table 그리기
static void fillParent(){
for(int i=1; i<K; i++){
for(int j=1; j<=N; j++){
parent[i][j] = parent[i-1][parent[i-1][j]];
}
}
}
// LCA 구하기
static int lca(int a, int b){
// 1. depth[a] >= depth[b] 가 되도록 조정
if(depth[a] < depth[b]) return lca(b, a);
// 2. 더 깊은 a를 2^K승 점프하여 depth를 맞추기
for(int i=K-1; i>=0; i--){
// 만약 depth가 5차이 난다면, 먼저 4를 선택하고, 이후 다시 1이 선택되므로 depth가 맞춰짐
if(Math.pow(2,i) <= depth[a] - depth[b]){
a = parent[i][a];
}
}
// 3. depth를 맞췄는데 같다면 종료
if(a == b) return a;
// 4. a-b 는 같은 depth이므로 2^K승 점프하여 공통부모 바로 아래까지 올라가기
for(int i=K-1; i>=0; i--){
if(parent[i][a] != parent[i][b]){
a = parent[i][a];
b = parent[i][b];
}
}
// 이후 공통부모 바로 아래에 a와 b값이 위치하므로 그것의 바로 한칸 위를 리턴해주기.
return parent[0][a];
}
}