플로이드-워셜 알고리즘 (Floyd-Warshall)
January 27, 2022
플로이드-워셜 알고리즘이란?
플로이드 워셜 알고리즘은 V개의 정점과 E개의 간선을 가진 가중 그래프 G에서 모든 정점사이의 최단경로를 구하는 알고리즘이다.
- 어떤 두 정점 사이의 최단경로는 특정한 경유지(K)를 거치거나 거치지 않는 경로 중 하나이다. (정점 A와 B의 최단경로는 A-K-B 또는 A- B 이다)
- 경유지 K를 거친다면 최단 경로를 이루는 부분 경로 역시 최단 경로이다. (A-B의 최단경로가 A-K-B라면 A-K 와 K-B도 최단경로이다.)
- cycle이 없다면 음수 가중치도 가능하다.
-
DP로 접근한다.
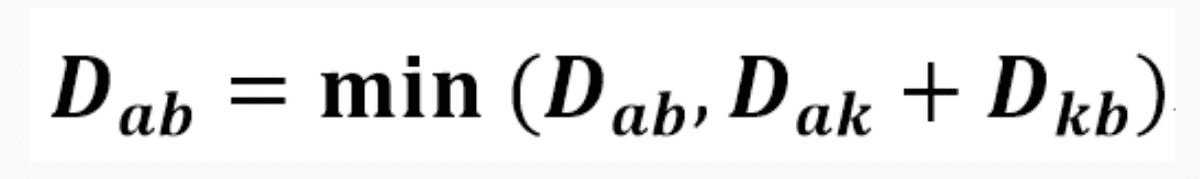
자바 코드
public class Main{
public static void main(String[] args){
// N은 정점의 개수
// M은 간선의 개수
int[][] graph = new int[N+1][M+1];
for(int i=1; i<=M; i++){
// 간선의 정보 저장
graph[출발점][도착점] = 가중치;
}
for(int i=1; i<=N; i++){
for(int j=1; j<=N; j++){
for(int k=1; k<=N; k++){
// j에서 k로 가는 중 j와 k가 자기 자신이 아닐때
// 경유지에 가는 경로가 있을 때
if(j != k && graph[j][i] != 0 && graph[i][k] != 0){
// j에서 k로 가는 경로가 없거나
// j에서 k로 가능 경로가 j에서 k로 가는중 i를 거치는것보다 클 경우
// 최단거리를 갱신한다.
if(graph[j][k] == 0 || graph[j][k] > graph[j][i] + graph[i][k]){
graph[j][k] = graph[j][i] + graph[i][k]
}
}
}
}
}
}
}모든 정점에 대해 모든 경유지로 삼아 확인하며 모든 간선을 체크하기때문에 for문이 3번 발생한다. 따라서 시간복잡도는 O(N^3)이다.